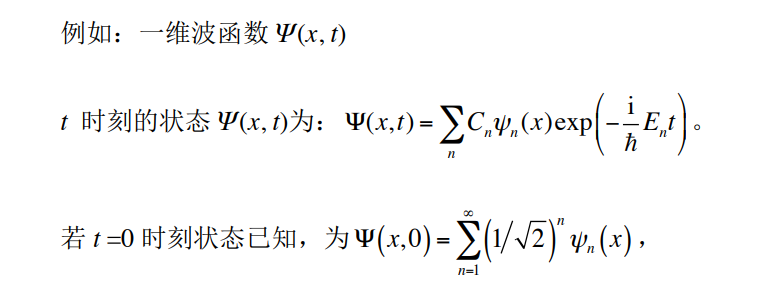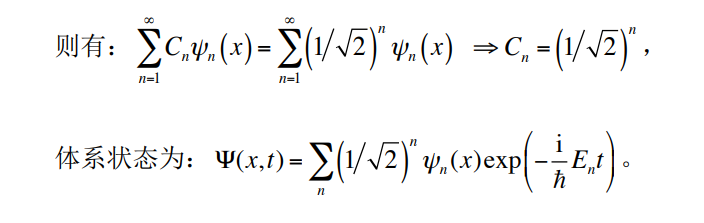Schrödinger equation
根据波粒二象性的假设,要描述一个微观粒子需要用到波函数,那么如何确定一个粒子的波函数?
1926年Schrödinger提(猜)出了薛定谔方程对此问题给出了解答。
微观粒子运动方程所需要的要求
- 波函数是态函数,即在
时刻,粒子有状态 ,若以此为初始条件去求得其之后的状态,则其后续状态与时间有关,方程中需要含有波函数对时间的一阶导数。 - 波函数要满足态叠加原理,即:若
与 都是波动方程的解,则 也需要是方程的解,这就要求方程是线性的,波动方程中没有与坐标相关的高次项或开方项(含有对坐标各阶导数的一次项)。 - 波动方程不应与其他状态参量相联系,不能含有E,P等参数。
相关推导
非相对论情形下自由粒子的薛定谔方程
自由粒子(不受外场作用)的波函数:
对时间一阶微分:
对坐标进行一阶微分: 一阶微分,即梯度算符,在直角坐标系下的表示
对坐标进行二阶微分:
结合(1)、(2)两式得到非相对论情形下的自由粒子的薛定谔方程:
非相对论情形下的一般形式的薛定谔方程
在外力的作用下粒子除了具有动能还有势能
非相对论情形下的定态薛定谔方程
定态指:能量不随时间变化的状态,概率密度也与时间无关。即用不含时的薛定谔方程来描述。
于是有:
代入薛定谔方程:
等式两边同时除以
由于概率密度和能量与时间无关
(a)式得解为
将常数C归结到波函数中,则
显而易见
即:[1]
空间波函数ψ(r)是由定态 Schrödinger 方程解出的,所以也称为定态波函数,也可看作是t=0时刻的定态波函数Ψ(r,0) 。
#体系的一般态
能量本征值方程一般有很多解,即存在很多个可能的不同的态,而体系可能的一般状态则为所有状态的叠加,即: